课程作业
课程名称:计算机语音技术
作业次数:第2次
学号:21281280
姓名:柯劲帆
班级:物联网2101班
指导老师:朱维彬
修改日期:2023年10月14日
---
## 1. 问题1
**语音信号由声学信号转换成离散的数字序列要经过那些过程？模数转换的指标是什么，之前为何要加抗混叠滤波器？**
语音信号由声学信号转换成离散的数字序列要经过以下过程：
1. 拾音：麦克风将语音信号从声波转换成模拟信号；
2. 放大：电路中放大器将模拟信号放大；
3. 抗混叠滤波：基于奈奎斯特采样定理，滤波器将原始信号中高于采样频率两倍的频率成分去除，避免频率混叠；
4. 模/数转换：将模拟信号离散化，转换成离散的数字序列，其中分两步：
1. 取样：等时间间隔取样，将信号在在时间上离散化；
2. 量化：在数值上离散化，将信号幅度转换成二进制序列表示的整数。
模数转换的指标有两个：
- 采样频率：$F_{\text{sample}} > 2 \times F_n $，需要满足奈奎斯特采样定理；
- 量化精度：
- 量化字长$B$：能将最大幅度量化成$2^B$等分，其决定了能够量化的幅度范围或精度。
- 噪声$e$：$e$的方差为$\sigma^2_e = \frac{1}{3}\left(\frac{\frac{2X_{\text{max}}}{2^B}}{2}\right)^2 = \frac{1}{3}\left(\frac{X_{\text{max}}}{2^B}\right)^2$，量化噪声工程估计为$\operatorname{SNR}\left(\text{dB}\right) = 6.02B-7.2$。
加抗混叠滤波器的原因：
根据奈奎斯特采样定理，如果采样频率$F_{\text{sample}}$小于两倍的最高频率成分$F_n$，那么在采样过程中，高于奈奎斯特频率的高频成分会混叠到基带频率，导致采样后的信号出现错误，如下图所示：
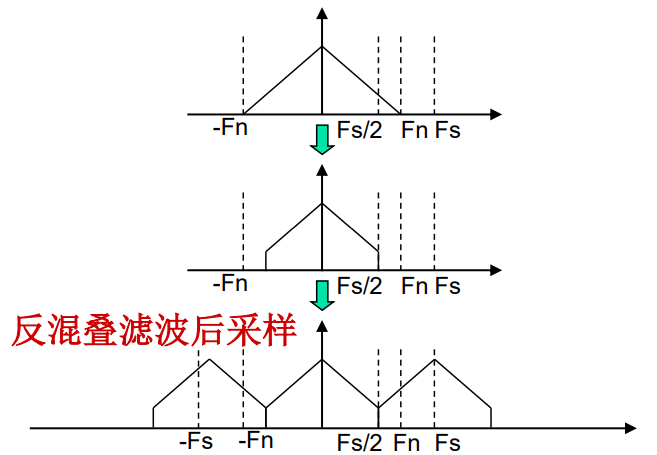
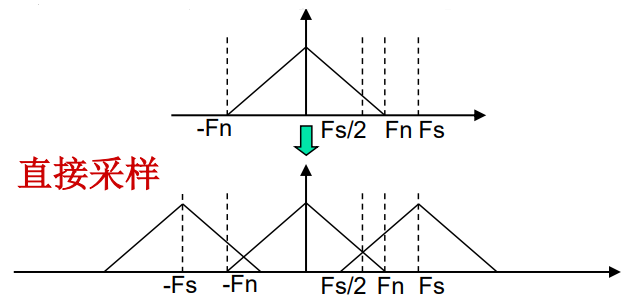因此需要加抗混叠滤波器，滤除信号中高于奈奎斯特采样频率的频率成分，确保在采样时不会出现混叠现象，如下图所示：
## 2. 问题2
**短时能量和短时过零率的定义，给出公式并加以说明。**
短时平均能量指在语音信号的不同时间段内，信号的能量或振幅的平均值。定义如下：
窗函数：
$$
w\left(n\right)=\left\{\begin{array}{ll}
1, & 0 \leq n \leq N-1 \\
0, & \text { 其它 }
\end{array}\right. \\
$$
短时平均能量：
$$
E_{n}=\sum_{m=-\infty}^{\infty}[x\left(m\right) w\left(n-m\right)]^{2}=\sum_{m=n-N+1}^{n}[x\left(m\right) w\left(n-m\right)]^{2}
$$
其中，$x^{2}\left( n \right) $表示语音信号在第$n$个时间段的平方振幅，$h\left(n-m\right)$表示窗函数的平方在不同时间偏移$m$下的取值。
令$h\left(n\right)=w^{2}\left(n\right)$，得到
$$
E_{n}=\sum_{m=-\infty}^{\infty} x^{2}\left(m\right) h\left(n-m\right)=x^{2}\left(n\right) \ast h\left(n\right)
$$
即$E_{n}$是语音信号在第$n$个时间段的平方振幅与窗函数平方的卷积。
其中窗函数可以有多种，常用的有：
1. 矩形窗
$$
h\left(n\right)=\left\{\begin{array}{ll}
1, & 0 \leq n \leq N-1 \\
0, & \text { 其它 }
\end{array}\right. \\
$$
2. 海明窗
$$
h\left(n\right)=\left\{\begin{array}{ll}
0.54 - 0.4\cos\left[2\pi n / \left(N - 1\right)\right], & 0 \leq n \leq N-1 \\
0, & \text { 其它 }
\end{array}\right. \\
$$
3. 汉宁窗
$$
h\left(n\right)=\left\{\begin{array}{ll}
0.5\left[1 - \cos\left(\frac{2\pi n}{N - 1}\right)\right], & 0 \leq n \leq N-1 \\
0, & \text { 其它 }
\end{array}\right. \\
$$
短时过零率指在语音信号的短时段内，信号穿过水平线（即振幅为0）的次数。定义如下：
窗函数：
$$
w\left(n\right)=\left\{\begin{array}{ll}
\frac{1}{2 N}, & 0 \leq n \leq N-1 \\
0, & \text { 其它 }
\end{array}\right. \\
$$
短时过零率：
$$
Z_{n}=\sum_{m=-\infty}^{\infty}\left|\operatorname{sgn}\left[x\left(m\right)\right]-\operatorname{sgn}\left[x\left(m-1\right)\right]\right| w\left(n-m\right) \\
\quad=\left|\operatorname{sgn}\left[x\left(n\right)\right]-\operatorname{sgn}\left[x\left(n-1\right)\right]\right| \ast w\left(n\right) \\
$$
其中$\operatorname{sgn}$是符号函数：
$$
\operatorname{sgn}\left(x\left(n\right)\right)=\left\{\begin{aligned}
1, & x\left(n\right) \geq 0 \\
-1, & x\left(n\right)<0
\end{aligned}\right.
$$
即先将信号幅度归一化为$1$（在水平线上方）和$-1$（在水平线下方），然后与窗函数进行卷积。
在噪声背景下，$\operatorname{sgn}$被修正为：
$$
\operatorname{sgn}\left(x\left(n\right)\right)=\left\{\begin{aligned}
1, & x\left(n\right) \geq \Delta \\
-1, & x\left(n\right)< -\Delta
\end{aligned}\right.
$$
以消除噪声的影响。
窗函数的作用是限制信号在时间和频率上的特性，确保在分析时局部信号的平稳性。窗函数可以防止频谱泄漏，提高分析的准确性。
## 3. 问题3
**语音信号的短时频谱的定义，如何提高短时频谱的频率分辨率？**
语音信号的短时频谱的定义：
短时频谱是指在语音信号的不同时间段内，信号的频率成分分布情况。
短时频谱可以通过对语音信号进行短时傅里叶变换计算得到，也就是将信号分割成短时段，然后对每个短时段进行傅里叶变换，得到该时段的频谱信息。
提高短时频谱的频率分辨率的方法：
增大窗函数时域窗长。
由测不准原理，窗函数时域窗长与其频域主瓣宽度的乘积不小于$\frac{1}{2}$，因此欲减小频域主瓣宽度（即频率分辨率），则需要提高窗函数时域窗长。
当然，也可以选择合适的窗函数与信号谱进行卷积，比如在同等分辨率条件下，矩形窗的窗长为海明窗窗长的$\frac{1}{2}$。
搜索资料发现，还可以使用高阶傅里叶变换方法提高短时频谱的频率分辨率，但代价是计算复杂度会增加。
## 4. 问题4
**请分析短时分析中窗函数的作用。**
- 选择分析的语音段。
- 将整个信号在短时段内截断，确保分析的语音段具有较好的时域特性。
- 时域表现为端点的截断效应，频域体现为旁瓣衰减程度。
- 时域：将信号在窗口之外置零，避免了窗口边界处的信号突变；
- 频域：窗函数的选择影响旁瓣的衰减程度，旁瓣衰减的情况决定频谱的分辨率。
- 改变窗的长度，折衷设置时间/频率分辨率。
- 窗函数的长度决定了分析的时间窗口长短。较短的窗口提供了较高的时域分辨率，但频率分辨率较低。较长的窗口则提供了较好的频率分辨率，但时域分辨率较低。因此，窗函数的长度是时域分辨率和频率分辨率之间的折衷。可以根据时域和频域的分辨率需求，选择合适的窗口长度。