课程作业
课程名称:计算机语音技术
作业次数:第3次
学号:21281280
姓名:柯劲帆
班级:物联网2101班
指导老师:朱维彬
修改日期:2023年11月1日
---
# 1. 问题1
**请说明同态分析的基本思想,并说明同态系统三个组成系统的功能。**
同态分析的基本思想是:由于系统中的信号是非加性信号,希望能把信号变成加性信号后进行操作,再还原原本的信号。实现方法由以下步骤:
1. 通过特征变换将非线性信号转化为线性信号
2. 对线性信号进行线性滤波处理
3. 再通过逆特征变换将处理后的线性信号转换回原来的非线性信号
相应的,同态系统由以下三个部分组成:
1. **特征系统**:通过对数变换,将非线性信号转化为线性信号。
2. **线性系统**:对线性信号进行滤波处理。
3. **逆特征系统**:通过指数变换,将滤波处理后的线性信号转换回原来的非线性信号形态。
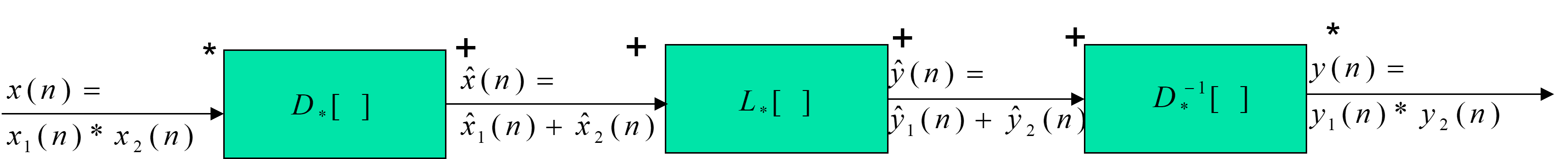
# 2. 问题2
**已知一语音时间序列$x\left(n\right)$,请写出其对应的复倒谱、倒谱$\hat{x}\left(n\right) $、$c\left(n\right) $的计算公式。**
复倒谱:
$$
\hat{x}\left(n \right)=\mathcal{F}^{-1}\left[\hat{X}\left(e^{j\omega}\right)\right]=\mathcal{F}^{-1}\left[\ln{X\left(e^{j\omega}\right)}\right]=\mathcal{F}^{-1}\left\{\ln{\mathcal{F\left[x\left(n\right)\right]} }\right\}
$$
倒谱:(复倒谱的实数部分)
$$
c\left(n \right)=\mathcal{F}^{-1}\left[\ln{\left|X\left(e^{j\omega}\right)\right|}\right]=\mathcal{F}^{-1}\left\{\ln{\left|\mathcal{F\left[x\left(n\right)\right]}\right|}\right\}
$$
# 3. 问题3
**请说明线性预测的基本概念,并用数学公式描述线性预测方程组的建立过程。**
线性预测指的是,根据语音样点值之间存在相关性,一个语音样点值可以用过去的若干样点值的线性组合,输入模型分析来逼近和预测。
线性预测方程为
$$
\hat{s}\left ( n \right ) = \sum_{i=1}^{P} a_i s\left ( n-i \right )
$$
其中$s\left(n\right)$是原语音信号,$\hat{s}\left ( n \right )$是预测信号,$a_i$是线性预测系数。
预测误差为
$$
e\left ( n \right ) = s\left ( n \right ) - \hat{s} \left ( n \right )
$$
均方误差准则
$$
E_n = \sum_{n}e^{2}\left ( n \right )
$$
对$a_i$求偏导,使得$E$最小
$$
\frac{\partial E}{\partial a_j} = 2\sum_{n}s\left(n\right)s\left(n-j\right)-2\sum_{i=1}^{p}a_i\sum_{n}s\left(n-i\right)s\left(n-j\right)=0
$$
构成线性方程组
$$
\sum_{n}s\left(n\right)s\left(n-j\right)=\sum_{i=1}^{p}a_i\sum_{n}s\left(n-i\right)s\left(n-j\right)
$$
即
$$
\sum_{i=1}^{p} a_i R_n\left( \left | j-i \right | \right) =R_n\left ( j \right ),\left ( 1\le j\le P \right )
$$
其中$R_n$是自相关函数。求解可得线性预测系数$a_1,a_2,a_3,\cdots ,a_p$。
# 4. 问题4
**已知语音信号的线性预测系数$a_i$,说明$\text{LPC}$谱的计算过程以及预测阶数$P$对$\text{LPC}$谱的影响。**
声道传递函数
$$
H\left ( z \right ) =\frac{G}{1-\sum_{i=1}^{P} a_iz^{-i}}
$$
代入$z = e^{j\omega}$,由$\text{Z}$域转换到频域,得到$\text{LPC}$谱
$$
H\left ( e^{j\omega} \right ) =\frac{G}{1-\sum_{i=1}^{P} a_ie^{-j\omega i}}
$$
预测阶数$P$对$\text{LPC}$谱的影响:
1. $P$决定了$\text{LPC}$模型的参数个数,$P$越大,能逼近信号谱的细节越多。
2. $P$越大,$\text{LPC}$谱上的共振峰个数越多,能反映出更多的共振峰信息。
3. 一般取$P$为$10\sim 14$阶,每个共振峰对应$2$阶,额外增加$2\sim 4$阶用于反映零点信息。
4. $P$的选择还要考虑分析帧长,要保证帧长大于$2$倍基音周期。