



| 原图 | 灰度反转 | |||
 |
 |
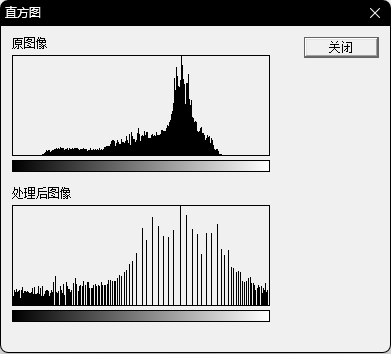
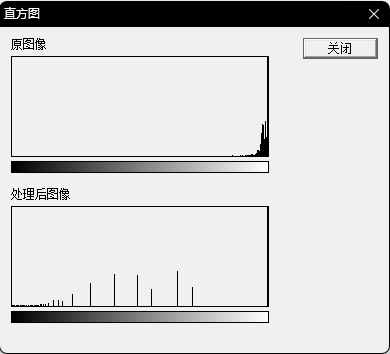
| 偏暗 | 正常 | 偏亮 | |
| 原图 |  |
 |
 |
| 直方图均衡化 |  |
 |
 |
| 直方图统计 | 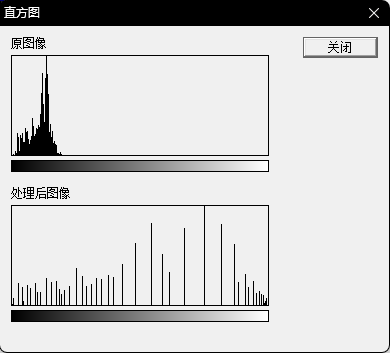 |
 |
 |
| 噪声 | 中值滤波 | 均值滤波 |
| 原图 |  |
|
| 加高斯噪声 |  |
 |
| 加椒盐噪声 |  |
 |
| 原图 | Sobel算子法 | Prewitt算子法 | Roberts算子法 | LoG算子法 |
 |
 |
 |
 |
 |
| 原图 | 医学伪彩色 | 遥感伪彩色 | |
 |
 |
 |
| 原图 | 二值化 | ||
 |
 |
| 原图 | 傅里叶变换 | 沃尔什变换 | 离散余弦变换 |
 |
 |
 |
 |