课程作业

课程名称:计算机语音技术

作业次数:第5次

学号:21281280

姓名:柯劲帆

班级:物联网2101班

课程教师:朱维彬

修改日期:2023年11月30日

1. 问题1

HMM利用有限状态刻画语音过程，请简要说明HMM三个基本参数，并如何用以刻画状态序列X与语音特征序列O间的关系-计算两者间的联合概率。

HMM：\lambda = f\left(A, B, \pi\right)

参数	含义
`\pi`	初始状态概率。$\pi=\left[\pi_1, \pi_2, \dots ,\pi_L\right]$，`\pi_j = P_r\left[x_1=S_j\right]`
`A`	状态转移概率矩阵。$A=\left[a_{ij}\right]$，`a_{ij}=P_r\left[x_t=S_j\mid X_{t-1}=S_i\right]`
`B`	观察值概率矩阵。$B = \left[b_i\left(o_t\right)\right]$，`b_i\left(o_t\right) = P_r\left[o_t\mid x_t=S_i\right]`

由给定的模型M，计算特征序列O与状态序列X的联合概率：

$t = 0$，根据初始状态概率向量$\pi$，选一初始状态$S_{X_0}$出现概率$\pi_{X_0}$；
根据B和状态$S_{X_0}$确定$o_t$的概率分布$b_{X_t}\left(o_t\right)$；
根据A和$S_{X_{t-1}}$确定转移到下一状态$S_{X_t}$的转移概率$a_{X_{t-1}X_{t}}$；
$t = t + 1$，如果$t<T$，跳转到2，否则结束。

状态序列X与语音特征序列O的联合概率为：


P\left(O, X\mid M\right)=\pi_{X_0}\prod_{t=1}^{T} a_{X_{t-1}X_t}b_{X_t}\left ( O_t \right )

2. 问题2

基于最大似然解码的语音识别系统可用公式$\hat{W}=\underset{W}{\mathrm{argmax}}P\left (O\mid W \right )P\left ( W \right ) $加以描述，请说明公式及其中符号的意义。

符号	意义
`\hat{W}`	要估计的最优单词序列，即通过最大似然解码得到的最可能的单词序列。
`O`	对语音信号短时分析，提取特征向量，形成观察序列。
`W`	转写的文字序列。
`P\left (O\mid W \right )`	在给定单词序列$W$的条件下，观测到语音信号$O$的概率。对应于声学模型，表示了语音信号与特定单词序列之间的关系。
`P\left ( W \right )`	单词序列$W$出现的先验概率，即在没有观测到语音信号的情况下，对单词序列的先验估计。对应于语言模型，表示了单词序列的语言结构信息。

整个公式$\hat{W}=\underset{W}{\mathrm{argmax}}P\left (O\mid W \right )P\left ( W \right ) $表示：在所有可能的单词序列$W$中，找到使得声学模型概率与语言模型概率之积最大化的序列，即为估计最优的单词序列。

3. 问题3

Viterbi常应用于确定HMM最优状态序列，请说明最优路径搜索及对应的最优完全路径概率计算过程。

初始化
```
\delta_1\left(i\right)=\pi_i b_i\left(y_1\right) \left(i=1, 2, \dots, L\right)
```
- $\delta_1(i)$：在时刻$t=1$，处于状态$i$的部分观察序列的最大概率。这是一个前向概率。
- $\pi_i$：初始时刻状态$i$的概率。
- $b_i(y_1)$：在状态$i$下生成观察符号$y_1$的概率。
计算概率、最优路径
```
\begin{array}{c}
\delta_{n+1}\left(j\right) = \underset{i}{\mathrm{max}}\left(\delta_n\left(i\right)A_{ij}\right)\cdot b_j\left(y_{n+1}\right)\\
\varphi_{n+1}\left(j\right)= \underset{i}{\mathrm{argmax}}\left(\delta_n\left(i\right)A_{ij}\right) \left(i, j=1,2, \dots, L\right) 
\end{array}
```
- $\delta_{n+1}(j)$：在时刻$t=n+1$，处于状态$j$的部分观察序列的最大概率。
- $\underset{i}{\mathrm{max}}\left(\delta_n(i)A_{ij}\right)$：在时刻$t=n$的状态$i$到$t=n+1$的状态$j$的转移概率的最大值。
- $A_{ij}$：从状态$i$转移到状态$j$的转移概率。
- $b_j(y_{n+1})$：在状态$j$下生成观察符号$y_{n+1}$的概率。
- $\varphi_{n+1}(j)$：在时刻$t=n+1$，处于状态$j$的部分观察序列的最大概率对应的状态$t=n$的最优路径的最后一个状态。
确定最优完全路径
```
\hat{l}_N = \underset{j}{\mathrm{argmax}}\left(\delta_N\left(j\right)\right)
```
- $\hat{l}_N$：在时刻$t=N$，具有最大概率的状态。
路径回溯
```
\hat{l}_n = \varphi_{n+1}\left(\hat{l}_{n+1}\right)
```
- $\hat{l}_n$：在时刻$t=n$，具有最大概率的状态。
- $\varphi_{n+1}(\hat{l}_{n+1})$：在时刻$t=n+1$，具有最大概率的状态$t=n$的最优路径的最后一个状态。

4. 问题4

传统的语音识别系统由4个主要模块构成：前端、声学模型、语言模型、解码。绘制由此构成的系统框图，说明模块功能及之间的关系。

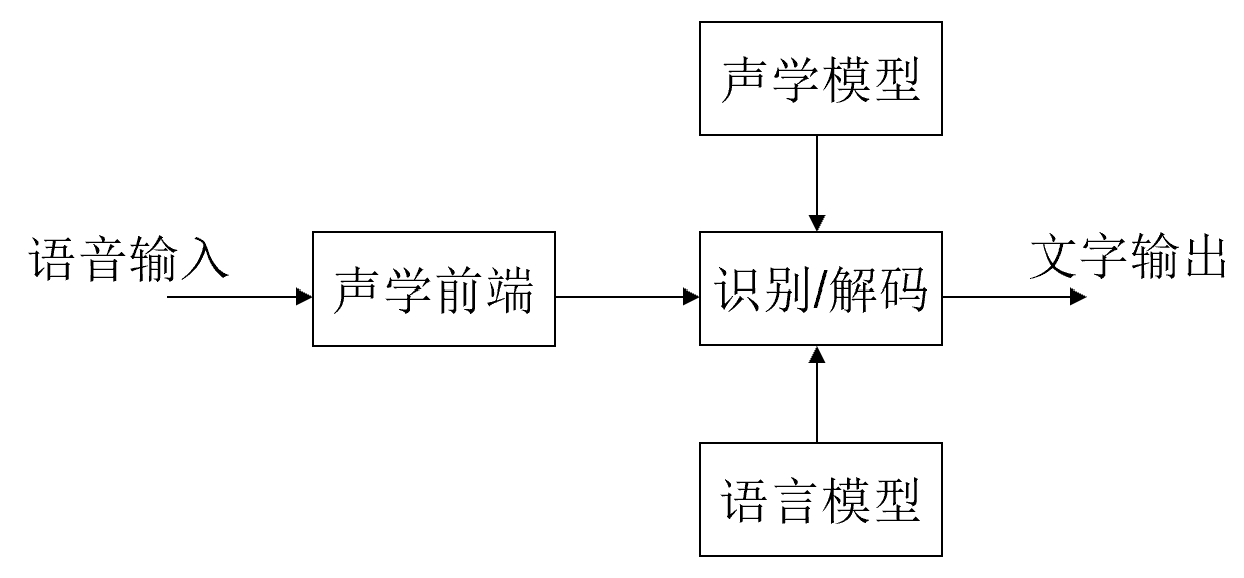
声学前端：将输入的语音信号转化为可供后续处理的特征向量
- 进行预处理、分帧和特征提取
声学模型：将语音信号的特征向量转化为注音符号
- 通常是基于HMM的统计模型
语言模型：将注音符号转化为转写文字
- 为解码器提供根据上下文预测下一个单词/音素的能力
识别/解码：搜索最大似然解
- 将声学模型和语言模型结合起来，根据这两个模型的输出进行最终的识别和解码

7.2 KiB Raw Permalink Blame History Unescape Escape

课程作业

1. 问题1

2. 问题2

3. 问题3

4. 问题4

7.2 KiB

Raw Permalink Blame History